Question

Find two values of "b" so that x^2 + b x + 6 can be factored into binomial factors.​

Answer 1

Given:

The expression is

`x^2+bx+6`

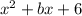
To find:

The values of b so that the given expression can be factored into binomials factors.

Solution:

An expression is
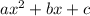`ax^2+bx+c` factorable if b is the sum of possible factors of ac.

We have,

`x^2+bx+6`

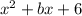
Here,
`a=1,b=b,c=6`.

`ac=(1)(6)`

`ac=6`

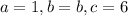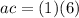
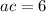
Some, factor forms of 6 are (1×6) and (2×3).

`1+6=7`

`2+3=5`

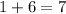
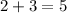
For b=7,

`x^2+7x+6=x^2+x+6x+6`

`x^2+7x+6=x(x+1)+6(x+1)`

`x^2+7x+6=(x+1)(x+6)`

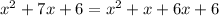
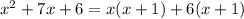
For b=5,

`x^2+5x+6=x^2+2x+3x+6`

`x^2+5x+6=x(x+2)+3(x+2)`

`x^2+5x+6=(x+2)(x+3)`

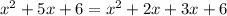
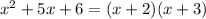
Therefore, the two possible values of b are 7 and 5.