Given:
The leading coefficient of a polynomial is 8.
Polynomial roots are 1 and 2.
The graph passes through the point (4,5).
To find:
The 3rd root and the equation of the polynomial.
Solution:
The factor form of a polynomial is:
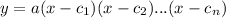
Where, a is a constant and
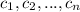 are the roots of the polynomial.
are the roots of the polynomial.
Polynomial roots are 1 and 2. So,
 and
and
 are the factors of the polynomial.
are the factors of the polynomial.
Let the third root of the polynomial by c, then
 is a factor of the polynomial.
is a factor of the polynomial.
The leading coefficient of a polynomial is 8. So, a=8 and the equation of the polynomial is:
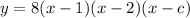
The graph passes through the point (4,5). Putting
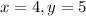 , we get
, we get
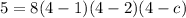
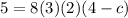
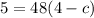
Divide both sides by 48.

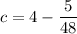
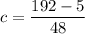

Therefore, the 3rd root on the polynomial is
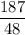 .
.