Question

Consider a teeter-totter that is made out of pine, shown below. A pineapple sits on

one side of the teeter-totter, a distance 1.23 m from the pivot point, while an apple
(non-pine) sits on the other side, a distance of 2.95 m from the pivot. If the
pineapple has a mass 121 g, what must the mass of the apple be in order to balance
the teeter-totter (ie, to maintain rotational equilibrium)?

Answer 1

Approximately
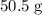`50.5\; {\rm g}` (rounded to three significant figures.)

Step-by-step explanation:

Let
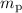`m_\text{p}` and
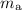`m_\text{a}` denote the mass of the pineapple and the apple, respectively.

Let
`r_{\text{p}}` denote the distance between the pineapple and the pivot. Let
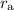`r_{\text{a}}` denote the distance between the apple and the pivot.

Because of gravity, both the pineapple and the apple would exert a normal force on the seesaw. The magnitude of that force is equal to the weight of the fruit. Let
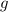`g` denote the gravitational field strength.

• Normal force from the pineapple:
  `F_\text{p} = m_{\text{p}}\, g`.
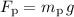• Normal force from the apple:
  `F_\text{a} = m_{\text{a}}\, g`.

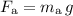Since these two forces are perpendicular to the seesaw, the magnitude of the torque exerted by the pineapple and the apple would be:

• From the pineapple:
  `\tau_{\text{p}} = F_\text{p}\, r_\text{p} = m_{\text{p}}\, g\, r_{\text{p}}`.
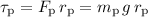• From the apple:
  `\tau_{\text{a}} = F_\text{a}\, r_\text{a} = m_{\text{a}}\, g\, r_{\text{a}}`.

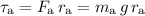For the seesaw to maintain a rotational equilibrium, these two torques need to balance each other. Thus:

`m_{\text{p}} \, g\, r_{\text{p}} = m_{\text{a}} \, g\, r_{\text{a}}`.

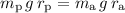Rewrite and simplify this equation to find an expression for the unknown mass of this apple,
`m_{\text{a}}`:

`\begin{aligned}m_{\text{a}} &= \frac{m_{\text{p}}\, g\, r_\text{p}}{g\, r_\text{a}} \\ &= \frac{m_{\text{p}}\, r_{\text{p}}}{r_\text{a}}\end{aligned}`.

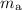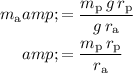Substitute in the values
`m_\text{p} = 121\; {\rm g}`,
`r_\text{p} = 1.23\; {\rm m}`, and
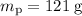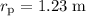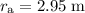`r_{\text{a}} =2.95\; {\rm m}` and evaluate:

`\begin{aligned}m_{\text{a}} &= \frac{m_{\text{p}}\, r_{\text{p}}}{r_\text{a}} \\ &= \frac{121\; {\rm g} * 1.23\; {\rm m}}{2.95\; {\rm m}} \\ &\approx 50.5\; {\rm g}\end{aligned}`.

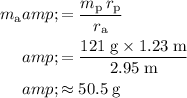Thus, the mass of the apple should be approximately
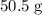`50.5\; {\rm g}`.