Answer:
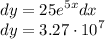
General Formulas and Concepts:
Math
- Rounding
- Euler's Number e - 2.71828
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Calculus
Derivatives
Derivative Notation
Differentials
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
eˣ Derivative:
![\displaystyle (dy)/(dx)[e^u] = u'e^u](https://img.qammunity.org/2022/formulas/mathematics/college/v0q6w311zgvwi7h2zdgnfoml3saddpybg1.png)
Explanation:
Part A
Step 1: Define
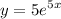
Step 2: Differentiate
- [Function] eˣ Derivative:
![\displaystyle (dy)/(dx) = (dy)/(dx)[5x] \cdot 5e^(5x)](https://img.qammunity.org/2022/formulas/mathematics/college/s41iyxrnejte9jso4pjmqtmf28hyvqf6x0.png)
- [Derivative] Basic Power Rule:
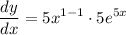
- [Derivative] Simplify:
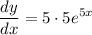
- [Derivative] Multiply:
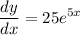
- [Derivative] [Multiplication Property of Equality] Isolate dy:
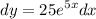
Part B
Step 1: Define
[Differential]
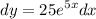
[Given] x = 3, dx = 0.4
Step 2: Evaluate
- Substitute in variables [Differential]:
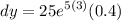
- [Differential] [Exponents] Multiply:
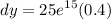
- [Differential] Evaluate exponents:
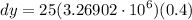
- [Differential] Multiply:
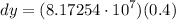
- [Differential] Multiply:
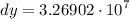
- [Differential] Round:
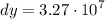
Topic: AP Calculus AB/BC (Calculus I/II)
Unit: Differentials
Book: College Calculus 10e