Question

The equation $y=-4.9t^2+3.5t+5$ describes the height (in meters) of a ball thrown upward at $3.5$ meters per second from $5$ meters above the ground, where $t$ is the time in seconds. In how many seconds will the ball hit the ground? Express your answer as a common fraction.

Answer 1

Explanation:

The position function is

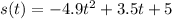`s(t)=-4.9t^2+3.5t+5` and if we are looking for the time t it takes for the ball to hit the ground, we are looking for the height of the ball when it is on the ground. Of course the height of anything on the ground is 0, so if we set s(t) = 0 and solve for t, we will find our answer.

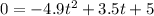`0=-4.9t^2+3.5t+5` and factor that however you are currently factoring in class to get that

t = -.71428 seconds or

t = 1.42857 seconds (neither one of those is rational so they can't be expressed as fractions).

We all know that time will never be a negative value, so the time it takes this ball to hit the ground is

1.42857 seconds (round how you need to).