Answer:
The coordinated points which quadrasects the line segments joining the points A and B are
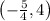 ,
,
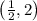 and
and
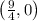 .
.
Explanation:
Let
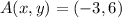 and
and
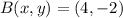 , when the line segment is quadrasected, it means that segment is divided into four equal parts. The locations are determined by the following expressions:
, when the line segment is quadrasected, it means that segment is divided into four equal parts. The locations are determined by the following expressions:
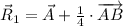 (1)
(1)
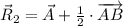 (2)
(2)
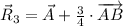 (3)
(3)
Where:
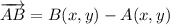
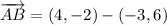

The coordinated points which quadrasects the line segments joining the points A and B are, respectively:
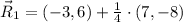

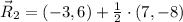

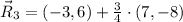
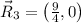
The coordinated points which quadrasects the line segments joining the points A and B are
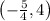 ,
,
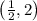 and
and
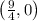 .
.