Solution :
Given :
a = (1, 2, 3, 4) , b = ( 4, 3, 2, 1), c = (1, 1, 1, 1) ∈
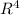
a). (a.2c)b + ||-3c||a
Now,
(a.2c) = (1, 2, 3, 4). 2 (1, 1, 1, 1)
= (2 + 4 + 6 + 6)
= 20
-3c = -3 (1, 1, 1, 1)
= (-3, -3, -3, -3)
||-3c|| =
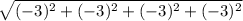
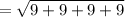
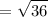
= 6
Therefore,
(a.2c)b + ||-3c||a = (20)(4, 3, 2, 1) + 6(1, 2, 3, 4)
= (80, 60, 40, 20) + (6, 12, 18, 24)
= (86, 72, 58, 44)
b). two vectors
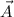 and
and
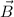 are parallel to each other if they are scalar multiple of each other.
are parallel to each other if they are scalar multiple of each other.
i.e.,
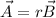 for the same scalar r.
for the same scalar r.
Given
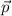 is parallel to
is parallel to
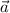 , for the same scalar r, we have
, for the same scalar r, we have
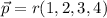
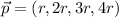 ......(1)
......(1)
Let
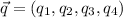 ......(2)
......(2)
Now given
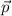 and
and
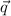 are perpendicular vectors, that is dot product of
are perpendicular vectors, that is dot product of
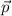 and
and
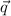 is zero.
is zero.
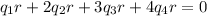
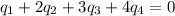 .......(3)
.......(3)
Also given the sum of
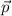 and
and
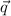 is equal to
is equal to
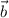 . So
. So
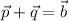
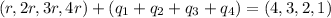
∴
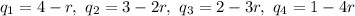 ....(4)
....(4)
Putting the values of
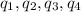 in (3),we get
in (3),we get
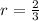
So putting this value of r in (4), we get
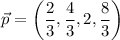
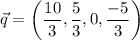
These two vectors are perpendicular and satisfies the given condition.
c). Given terminal point is
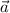 is (-1, 1, 2, -2)
is (-1, 1, 2, -2)
We know that,
Position vector = terminal point - initial point
Initial point = terminal point - position point
= (-1, 1, 2, -2) - (1, 2, 3, 4)
= (-2, -1, -1, -6)
d).
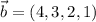
Let us say a vector
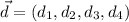 is perpendicular to
is perpendicular to
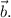
Then,
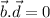
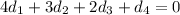
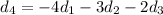
There are infinitely many vectors which satisfies this condition.
Let us choose arbitrary
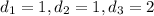
Therefore,
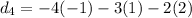
= -3
The vector is (-1, 1, 2, -3) perpendicular to given