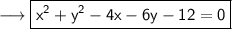Answer:
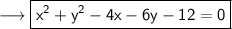
Explanation:
Here we are given the radius of circle as 5cm and the centre of the circle is (2,3) . We need to find the equation of the circle. Here we can yse the Standard equation of circle to find the equation .
Standard equation of circle :-
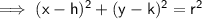
- where (h,k) is the centre and r is radius .
Substitute the respective values ,
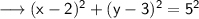
Simplify the whole square ,
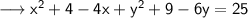
Rearrange and add the constants ,
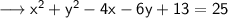
Subtract 25 on both sides ,
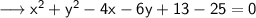
Simplify ,