Question

Find an equation of the line that is the perpendicular bisector of the line segment joining the points (6,2) and (18,6)

Answer 1

y= -3x +40

Explanation:

Properties of perpendicular bisector:

• perpendicular to the given line

• cuts through the center of the given line

The equation of a line can be written in the form of y=mx +c, where m is the gradient and c is the y -intercept.

Let's find the gradient of the given line first.

`\boxed{gradient = (y1 - y2)/(x1 - x2) }`

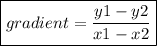
Gradient of given line

`= (6 - 2)/(18 - 6)`

`= (4)/(12)`

`= (1)/(3)`

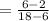
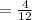
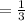
The product of the gradients of perpendicular lines is -1.

m(⅓)= -1

m= -1(3)

m= -3

Substitute m= -3 into the equation:

y= -3x +c

To find the value of c, substitute a pair of coordinates in which the perpendicular bisector passes through into the equation. Since perpendicular bisectors passes through the center of the segment, we can find the point in which the perpendicular bisector passes through using the mid- point formula.

`\boxed{midpoint = ( (x1 + x2)/(2) , (y1 + y2)/(2) )}`

Midpoint

`= ( (6 + 18)/(2) , (6 + 2)/(2) )`

`= ( (24)/(2) , (8)/(2) )`

`= (12,4)`

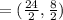
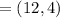
y= -3x +c

when x= 12, y= 4,

4= -3(12) +c

4= -36 +c

c= 4 +36

c= 40

Thus, the equation of the perpendicular bisector is y= -3x +40.