Question

You decide to set aside $120 a month for your future. Assuming an interest rate of 6.35%, how much will you have after 25 years? How much more would you have if you invested for 30 years?

Answer 1

After 20 years you will have "$87,784.99" and after 30 years you will have "$41,151.55".

Step-by-step explanation:

The give values are:

After 25 years,

Cash Flow per period,

C = $120

Interest rate per period,

i =
`(6.35 \ percent)/(12)`

=
`0.52916667 \ percent`

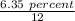
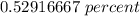
Number of period,

n =
`25* 12`

=
`300`

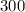
The future value will be:

=
`C* ( [(1+i)^n-1])/(i)`

On substituting the given values, we get

=
`(120[ (1+0.0052916667)^(300) -1])/(0.0052916667)`

=
`120[((4.8711 -1))/(0.0052916667) ]`

=
`87,784.99` ($)

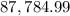After 30 years,

Cash Flow per period,

C = $120

Interest rate per period,

i =
`(6.35 \ percent)/(12)`

=
`0.52916667 \ percent`

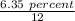
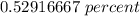
Number of period,

n =
`30* 12`

=
`360`

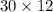
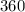
The future value will be:

=
`C* ( [(1+i)^n-1])/(i)`

On substituting the given values, we get

=
`(120[ (1+0.0052916667)^(360) -1] )/(0.0052916667)`

=
`(120[ (1.0052916667)^(360) -1])/(0.0052916667)`

=
`120[((6.6857 -1))/(0.0052916667) ]`

=
`128,936.54` ($)

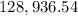Thus

You will have:

=
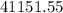`128936.54-87784.99`

=
`41151.55` ($)