Answer:
The given points isn't define a parallelogram.
Explanation:
As we know,
⇒ The opposite sides of a parallelogram are equal.
The given points are:
(x1, y1) = M(2,4)
(x2, y2) = I(1,2)
(x3, y3) = L(5,1)
(x4, y4) = K(4,−1)
Now,
On applying the Distance formula, we get
MI =
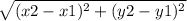
On substituting the given values, we get
=
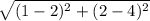
=
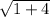
=
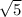
IL =
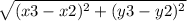
=
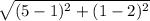
=
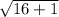
=
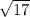
LK =
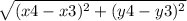
=
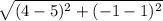
=
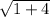
=
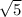
KM =
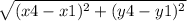
=
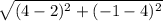
=
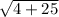
=
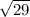
Here, MI = LK = √5
IL ≠ KM