Answer:
b < c < a < d
Explanation:
P.S - The exact question is -
Given - Suppose x is a real number with 0 < x <
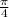 . Set a = sin(
. Set a = sin(
 - x) ,
- x) ,
b = cos(
 + x) , c = sin( x -
+ x) , c = sin( x -
 ) , d = cos(2
) , d = cos(2
 - x)
- x)
To find - Arrange the values of a, b, c, d in increasing order , and explain
how you determined their order.
Proof -
Firstly draw a unit circle where you indicate the following
A = ( cos(x), sin(x) )
B = ( cos(
 - x) , sin (
- x) , sin (
 - x) )
- x) )
C = ( cos(
 + x), sin (
+ x), sin (
 + x) )
+ x) )
D = ( cos (2
 - x) , sin (2
- x) , sin (2
 - x) )
- x) )
As we have given that 0 < x <
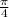
⇒sin (x) and cos(x) are positive and sin(x) < cos(x)
The figure is as follows :
Now
By seeing point B , we can say that
sin (
 - x) = sin (x) = a
- x) = sin (x) = a
By seeing point C , we can say that
cos(
 + x) = -cos (x) = b
+ x) = -cos (x) = b
By seeing point C , we can say that
sin( x -
 ) = -sin(x) = c
) = -sin(x) = c
By seeing point D , we can say that
cos(2
 - x) = cos(x) = d
- x) = cos(x) = d
As sin(x) < cos(x) ⇒ a < d
-sin(x) > -cos(x) ⇒ c > b ⇒ b< c
and as we know that -sin(x) < sin(x) ⇒ c < a
∴ we get
b < c < a < d