Hi there!
We can use the equation for gravitational force:
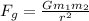
Fg = force due to gravity (N)
m1, m2 = masses of objects (kg)
r = distance between the center of mass of the objects (m)
G = gravitational constant
1.
Using the equation:

The force would be 9 times larger.
2. (Repeat?)
3.
The square of distance is inversely related, so:
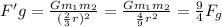
The force is 9/4ths times larger.
4.
Combining:
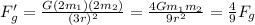
The force is 9/4ths times larger.
5.
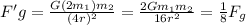
The force is 1/8th the original.
6.
Equation for gravitational field:
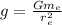
g = acceleration due to gravity (m/s²)
G = gravitational constant
me = mass of earth (kg)
re = radius of earth (m)
With the following transformations:

The acceleration due to gravity is 18 times as large.