Question

The average 30- to 39-year old man is 69.5 inches tall, with a standard deviation of 2.7 inches, while the average 30- to 39-year old woman is 64.2 inches tall, with a standard deviation of 3.2 inches. Who is relatively taller based on their comparison to their gender, LeBron James at 81 inches or Candace Parker at 76 inches?

a) Candace is relatively taller because she has a larger z-score.
b) LeBron is relatively taller because he has a larger z-score.
c) LeBron is relatively taller because he has a smaller z-score.
d) Candace is relatively taller because she has a smaller z-score.

Answer 1

b) LeBron is relatively taller because he has a larger z-score.

Explanation:

Z-score:

In a set with mean
`\mu` and standard deviation
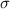`\sigma`, the z-score of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

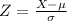
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.

LeBron James:

Height of 81 inches, while the average 30- to 39-year old man is 69.5 inches tall, with a standard deviation of 2.7 inches, which means that we have to find Z when
`X = 81, \mu = 69.5, \sigma = 2.7`

`Z = (X - \mu)/(\sigma)`

`Z = (81 - 69.5)/(2.7)`

`Z = 4.26`

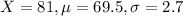
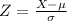
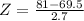
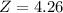
Candace Parker:

Height of 76 inches, while the average 30- to 39-year old woman is 64.2 inches tall, with a standard deviation of 3.2 inches. This means that we have to find Z when
`X = 76, \mu = 64.2, \sigma = 3.2`

`Z = (X - \mu)/(\sigma)`

`Z = (76 - 64.2)/(3.2)`

`Z = 3.69`

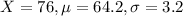
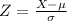
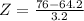
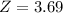
Who is relatively taller?

Due to the higher z-score, LeBron James, and thus, the correct answer is given by option b.