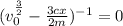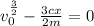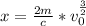Answer:
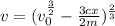
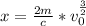
Step-by-step explanation:
Given
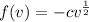
To start with, we begin with

Substitute the expression for F
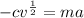

Acceleration (a) is:
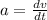
So, the expression becomes:

-----------------------------------------------------------------------------------------
Velocity (v) is:
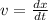 --- distance/time
--- distance/time
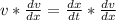
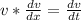
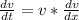
--------------------------------------------------------------------------------------------
So, we have:

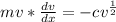
Divide both sides by
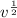
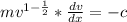
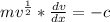
Divide both sides by m

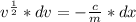
Integrate:
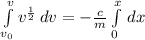
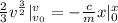
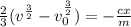
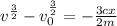

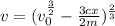
Next, is to get the maximum velocity by distance x.
To do this, we find the derivation by x

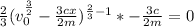
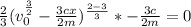
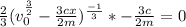
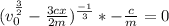
Divide both sides by
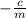
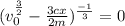
Take cube roots of both sides