Exponential functions exhibit a pattern where the independent variable, typically denoted as (x), is an exponent. These functions have a consistent rate of growth or decay, and their graphs form a distinctive shape, either exponential growth (when the base is greater than 1) or exponential decay (when the base is between 0 and 1).
Exponential functions are characterized by the presence of a variable as an exponent. The general form of an exponential function is
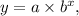 where (a) is the initial value or y-intercept, (b) is the base, and (x) is the independent variable. The pattern of exponential functions involves a consistent multiplicative rate of change due to the exponent. When the base (b) is greater than 1, the function demonstrates exponential growth, indicating that the output increases rapidly.
where (a) is the initial value or y-intercept, (b) is the base, and (x) is the independent variable. The pattern of exponential functions involves a consistent multiplicative rate of change due to the exponent. When the base (b) is greater than 1, the function demonstrates exponential growth, indicating that the output increases rapidly.
Conversely, when (b) is between 0 and 1, the function displays exponential decay, showcasing a gradual decrease. The graphical representation of exponential functions reveals a distinct pattern. In the case of exponential growth, the graph rises sharply, becoming steeper as (x) increases.
Exponential decay, on the other hand, results in a graph that descends gradually, approaching but never reaching the x-axis. Understanding this pattern is crucial for interpreting data involving exponential relationships, such as population growth, compound interest, or radioactive decay. The consistent rate of change dictated by the exponent distinguishes exponential functions and contributes to their applicability in modeling various natural phenomena and processes.