Answer:
a) 0.0465 = 4.65% probability that in one upperclassman House at MIT, enough students are vaccinated to achieve herd immunity.
b)
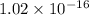 probability that herd immunity is achieved in all 12 Houses.
probability that herd immunity is achieved in all 12 Houses.
c) We needed that
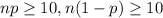 , which was achieved.
, which was achieved.
Explanation:
To solve this question, we need to understand the binomial distribution, normal probability distribution and the central limit theorem.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

In which
 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.

And p is the probability of X happening.
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the zscore of a measure X is given by:
, the zscore of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
Central Limit Theorem
For a proportion p in a sample of size n, as long as
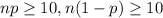 the sampling distribution of the sample proportion will be approximately normal with mean
the sampling distribution of the sample proportion will be approximately normal with mean
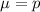 and standard deviation
and standard deviation
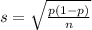
a) Suppose that 94% of undergraduate students in the United States report having received two doses of the MMR vaccine. What is the probability that in one upperclassman House at MIT, enough students are vaccinated to achieve herd immunity? There are approximately 400 students in any house.
We have that
 . So
. So
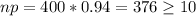
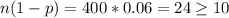
The standard deviation is:

The probability is 1 subtracted by the pvalue of Z when X = 0.96. So

By the Central Limit Theorem
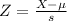
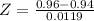
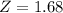
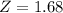 has a pvalue of 0.9535
has a pvalue of 0.9535
1 - 0.9535 = 0.0465 = 4.65% probability that in one upperclassman House at MIT, enough students are vaccinated to achieve herd immunity.
b) Calculate the probability that herd immunity is achieved in all 12 Houses.
Now, we use the binomial distribution. This is
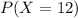 when
when
 with
with
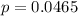 . So
. So

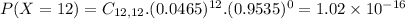
 probability that herd immunity is achieved in all 12 Houses.
probability that herd immunity is achieved in all 12 Houses.
c) Discuss the validity of the assumptions required to make the calculation in part i.
We needed that
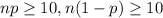 , which was achieved.
, which was achieved.