Answer:
a. Min Z = 2x₁ + 2.50x₂ + 3x₃
Subject to constraints :
3x₁ + 2x₂ + 4x₃ ≤ 128 .......(1)
3x₁ + x₂ + 3x₃ ≤ 160 ........(2)
x₁ + 0x₂ + 2x₃ ≤ 32 .........(3)
6x₁ + 8x₂ + 4x₃ ≤ 256 .........(4)
3x₁ + 2x₂ + 4x₃ ≥ 64 ..........(5)
3x₁ + x₂ + 3x₃ ≥ 80 ..........(6)
x₁ + 0x₂ + 2x₃ ≥ 16 ...........(7)
6x₁ + 8x₂ + 4x₃ ≥ 128 ............(8)
x₁ ≤ 15 ...........(9)
x₂≤ 15 ...........(10)
x₃ ≤ 15 ...........(11)
x₁ , x₂, x₃ ≥ 0
b. x₁ = 15 , x₂ = 9.5 , x₃ = 8.5
c. The optimal solution is Z = 79.25
Step-by-step explanation:
Given - The table is as follows :
- Nutrient Feed 1 Feed 2 Feed 3
- A 3 2 4
- B 3 1 3
- C 1 0 2
- D 6 8 4
The minimum requirement per cow each month is 4 pounds of nutrient A, 5 pounds of nutrient B, 1 pound of nutrient C, and 8 pounds of nutrient D. However, cows should not be fed more than twice the minimum requirement for any nutrient each month. Additionally, the ranch can only obtain 1,500 pounds of each type of feed each month. Because there are usually 100 cows at the beef-up ranch at any given time, this means that no more than 15 pounds of each type of feed can be used per cow each month.
To find - a. Formulate a linear programming problem to determine how
much of each type of feed a cow should be fed each month.
b. Create a spreadsheet model for this problem, and solve it using
Solver.
c. What is the optimal solution?
Proof -
a.
Let feed 1 per cow per month = x₁
feed 2 per cow per month = x₂
feed 3 per cow per month = x₃
Now,
As given, The cost per pound of feeds 1,2, and 3 are $2.00, $2.50, and $3.00, respectively.
So, we have to minimize the cost , Z = 2x₁ + 2.50x₂ + 3x₃
Subject to constraints :
3x₁ + 2x₂ + 4x₃ ≤ 4(32)
3x₁ + x₂ + 3x₃ ≤ 5(32)
x₁ + 0x₂ + 2x₃ ≤ 1(32)
6x₁ + 8x₂ + 4x₃ ≤ 8(32)
∴ we get
Min Z = 2x₁ + 2.50x₂ + 3x₃
Subject to constraints :
3x₁ + 2x₂ + 4x₃ ≤ 128 .......(1)
3x₁ + x₂ + 3x₃ ≤ 160 ........(2)
x₁ + 0x₂ + 2x₃ ≤ 32 .........(3)
6x₁ + 8x₂ + 4x₃ ≤ 256 .........(4)
Now, as given
However, cows should not be fed more than twice the minimum requirement for any nutrient each month.
∴ we have
3x₁ + 2x₂ + 4x₃ ≥
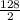
3x₁ + x₂ + 3x₃ ≥
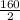
x₁ + 0x₂ + 2x₃ ≥
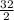
6x₁ + 8x₂ + 4x₃ ≥
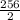
and also
No more than 15 pounds of each type of feed can be used per cow each month.
⇒x₁ , x₂, x₃ ≤ 15
So,
The LPP model becomes
Min Z = 2x₁ + 2.50x₂ + 3x₃
Subject to constraints :
3x₁ + 2x₂ + 4x₃ ≤ 128 .......(1)
3x₁ + x₂ + 3x₃ ≤ 160 ........(2)
x₁ + 0x₂ + 2x₃ ≤ 32 .........(3)
6x₁ + 8x₂ + 4x₃ ≤ 256 .........(4)
3x₁ + 2x₂ + 4x₃ ≥ 64 ..........(5)
3x₁ + x₂ + 3x₃ ≥ 80 ..........(6)
x₁ + 0x₂ + 2x₃ ≥ 16 ...........(7)
6x₁ + 8x₂ + 4x₃ ≥ 128 ............(8)
x₁ ≤ 15 ...........(9)
x₂≤ 15 ...........(10)
x₃ ≤ 15 ...........(11)
x₁ , x₂, x₃ ≥ 0
b.)
We use simplex method calculator to solve this LPP Problem
we get
x₁ = 15 , x₂ = 9.5 , x₃ = 8.5
c.)
The optimal solution is Z = 79.25