Answer:
Explanation:
If we are looking for the ratio of the area of the inner square to the area of the outer square, that means that we need the areas of each of these squares, and we need to find the areas without any numbers. But that's ok; the answer they want is not a number answer. The answer will have a's and b's in it instead of numbers.
First the area of the inner square. Here we go:
Look at the triangle in the lower left corner of this coordinate plane. It is a right triangle. The height of it is b. That's because the height is a "y" thing and the y-coordinates of each of those sets of coordinates is b and 0. The height is then b - 0 = b.
The length of the base is a - b. That's because the length is an "x" thing and the x-coordinates of each of those sets of coordinates is (a - b) and 0. The length is then a - b - 0 = a - b.
Now we need the length of the hypotenuse which also serves as one of the sides of the inner square. Using Pythagorean's Theorem, we can find the length of the hypotenuse, which I will label as "?":
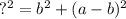 and
and
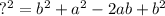 and
and
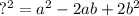 so
so
?, the length of the hypotenuse, is
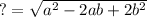 and now we can use that to find the area of the inner square. The formula for a square's area is
and now we can use that to find the area of the inner square. The formula for a square's area is
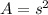 so
so
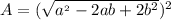 which gives us finally:
which gives us finally:
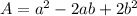 **
**
Now for the outer square. Those blue triangles you see are all congruent. We can use the side lengths for the triangles we found above to find the length of a side of the outer square. One side of the outer square is made up of one base length of these triangles and one height. We found the base length to be (a - b) and the height to be b; therefore, the length of one side of the outer square is b + (a - b) which is just "a". That's is, just a length of "a". The area is found by multiplying this side length by itself, so the area of the outer square is
A = a²
The ratio of the area of the inner to the outer is:
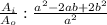 and that does not reduce.
and that does not reduce.