Question

A professor has two daughters that he hopes will one day go to college. Currently, in-state students at the local University pay about $21,225.00 per year (all expenses included). Tuition will increase by 3.00% per year going forward. The professor's oldest daughter, Sam, will start college in 16 years, while his youngest daughter, Ellie, will begin in 18 years. The professor is saving for their college by putting money in a mutual fund that pays about 9.00% per year. Tuition payments are at the beginning of the year and college will take 4 years for each girl. (Sam's first tuition payment will be in exactly 16 years)

The professor has no illusion that the state lottery funded scholarship will still be around for his girls, so how much does he need to deposit each year in this mutual fund to successfully put each daughter through college. (ASSUME that the money stays invested during college and the professor will make his last deposit in the account when Sam, the OLDEST daughter, starts college.)

Answer Format: Currency: Round to: 2 decimal places.

Answer 1

It will make yearly deposits of $ 6,053.60

Step-by-step explanation:

First, we have two phases:

the first which is the accumulation phase:

<---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|--->

^

which lasts until Sam's 1st year.

Then, we have the withdrawals phase

Graduation of Ellie

<---|----|----|----|----|----|---->

^Sam 1st year

^Ellie 1st year

We solve for the value of sam's first college year.

21,225 (1.03)^16 = 34,059.89

Then we solve for the present value of a growing annuity:

`\displaystyle (P)/(r-g) \left[1 - \left((1+g)/(1+r)\right)^n \right] \\P = $first payment\\r = interest\\g= growth\\n = time`

`\displaystyle (34059.89)/(0.09-0.03) \left[1 - \left((1+0.03)/(1+0.09)\right)^4 \right]`

PV = 115,043.63

Then we do the same with Ellie:

P $36,134.1373 (we adjust by two years)

r 0.09

g 0.03

n 4

PV 122,049.78

and then, we adjust for the 2-years difference:

122,049.78 / 1.09^2 = 102726.8613

Value of tuiton cost in 16 years for both daughters:

115,043.63 + 102,726.86 = 217,770.49

Now we solve for the yearly payment of an annuity due ( as the professor pays at the beginning) of 16 years:

Installment of a future annuity

`FV / \displaystyle ((1+r)^(time) +1)/(rate)(1+rate) = C\\`

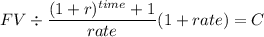
FV $217,770.49

time 16

rate 0.09

`217770.49 / ((1+0.09)^(16)-1 )/(0.09) = C\\`

C $ 6,053.602