Question

A medical researcher wishes to investigate the effectiveness of exercise versus diet in losing weight. Two groups of 25 overweight adult subjects are used, with a subject in each group matched to a similar subject in the other group on the basis of a number of physiological variables. One of the groups is placed on a regular program of vigorous exercise but with no restriction on diet, and the other is placed on a strict diet but with no requirement to exercise. The weight losses after 20 weeks are determined for each subject, and the difference between matched pairs of subjects (weight loss of subject in exercise group-weight loss of matched subject in diet group) is computed. The mean of these differences in weight loss is found to be -2 lb with standard deviation s = 6 pounds.

Is this evidence of a difference in mean weight loss for the two methods? To test this, consider the population of differences (the weight loss an overweight adult would experience after 20 weeks on the exercise program minus the weight loss the same adult would experience after 20 weeks on the strict diet). Let μ be the mean of this population of differences and assume their distribution is approximately Normal. Find the P-value for this matched pairs t-test.

Answer 1

Explanation:

From the given information;

The null and alternative hypothesis is:

`\mathbf{H_o: \mu =0}`

`\mathbf{H_a: \mu \\e 0}`

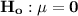
sample mean x = -2

population mean = 0

SD = 6

sample size n = 25

Using t-test statistics:

`t = (x- \mu)/((\sigma)/(√(n)))`

`t = (-2- 0)/((6)/(√(25)))`

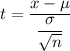
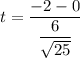
t = -1.667

P-value = P(t ≤ -1.667) + P(t ≥ 1.667)

P-value = 0.1086

Since P-value is greater than
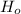`H_o` , we fail to reject
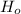`H_o`.