Question

Ross walked 3 m east and 6 m north. How far is he from the starting point

Answer 1

3 sqrt(5) meters

Explanation:

This is a right triangle so we can use the Pythagorean theorem.

a^2 +b^2 = c^2 where a and b are the legs and c is the hypotenuse

3^2+6^2 = c^2

9+36 = c^2

45 = c^2

Taking the square root

sqrt(45) = sqrt(c^2)

sqrt(9*5) = c

sqrt(9) sqrt(5) =c

3sqrt(5) = c

Answer 2

`\boxed{\large{\bold{\blue{ANSWER~:) }}}}`

Given:-

• Ross walked 3 m east and 6 m north.

Find:-

• How far is she from the starting point?

solution:-

Ross walked 3 m east and 6 m north.

so her path is a right angle triangle path.

we know that,

in a right angle triangle, According to the Pythagorean theorom,

`\boxed{\sf{l^2+b^2=h^2 }}`

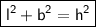
where

• l= legs
• b=base
• h=hypotenuse

According to the question,

• 
  `\sf{3^2+6^2=f^2 }`

• 
  `\sf{9+36=f^2 }`

• 
  `\sf{ f^2=45 }`

• 
  `\sf{f=√(45) }`

• 
  `\sf{f=3√(5) }`

Therefore:-

he is
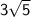`\sf{3√(5) }` far from the starting point