Answer:
The value of the test statistic is -3.14.
Explanation:
Test statistic:
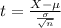
In which X is the sample mean,
 is the expected value,
is the expected value,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
A company advertises that its cans of caviar each contain 100 g of their product.
This means that

They calculate a sample mean weight of 99 g and a sample standard deviation of 0.9 g. Sample of 8 cans.
This means that
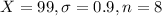
So the test statistic will be given by:
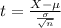
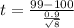
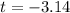
The value of the test statistic is -3.14.