Answer:
a. p = 0.25
b. n = 10, p = 0.25.
c. n = 10, p = 0.25.
d. n = 20, p = 0.25.
Explanation:
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

In which
 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.

And p is the probability of X happening.
a. For any single question on the quiz, what is p = chance of a correct guess?
4 options, 1 of which is correct. So

So p = 0.25.
b. Let X = number of correct guesses that Isabelle makes. What are the values of n and p for the binomial distribution that describes X?
Should be Ed here.
Ed guesses answers for the first 10 questions
This means that
 .
.
p is the same, so n = 10, p = 0.25.
c. Let Y = number of correct guesses that Taylor makes. What are the values of n and p for the binomial distribution that describes Y?
10 question, so
 , p is the same.
, p is the same.
d. Consider X + Y = total correct guesses that Isabelle and Taylor make. What are the values of n and p for the binomial distribution that describes X + Y?
20 questions, so

10 for Ed, with 0.25 probability, 10 for Taylor, with 0.25 probability. So
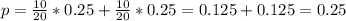
So n = 20, p = 0.25.