Question

According to the National Association of Realtors, it took an average of three weeks to sell a home in 2017. Suppose data for the sale of 39 randomly selected homes sold in Greene County, Ohio, in 2017 showed a sample mean of 3.6 weeks with a sample standard deviation of 2 weeks. Conduct a hypothesis test to determine whether the number of weeks until a house sold in Greene County differed from the national average in 2017. Use α = 0.05 for the level of significance, and state your conclusion.

a. State the null and alternative hypothesis.
b. Find the value of the test statistic.
c. Find the p-value.
d. State your conclusion.

Answer 1

Here, given :

Sample size, n = 39

Sample mean,
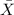`$\bar X$` = 3.6

Standard deviation of the sample, s =2

The population mean,
`$\mu_0 = 3$`

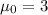
The significance level,
`$\alpha = 0.05$`

a). Therefore the hypothesis is :

`$H_0 : \mu = 3 \text{ Vs} \ H_a: \mu \\eq 3$`

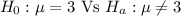
b). The test statics is given as :

`$t = (\bar X - \mu_0)/((s)/(\sqrt n)) \rightarrow t_(n-1)$`

`$t = \frac{3.6-3}{\frac{2}{\sqrt {39}}} $`

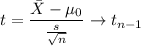
= 1.873

c). The p- value is given by :

`$P(t_(d.f)>|t_(stat)|)$`

`$=P(t_(39-1)> 1.873)$`

`$=0.0688$`

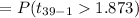
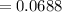
d). The conclusion :

In this case, the p-value is
`$0.688 > \alpha=0.05$`

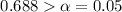
So, we do not reject
`$H_0$`.

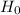Therefore, we conclude that it is not a statistically significant difference between national average time for selling a home and the mean time for selling in Greene County.