Answer:
The 90% confidence interval for the mean reduction in systolic blood pressure is between 22.66 and 40.14.
Explanation:
Subtraction of normal variables:
When we subtract normal variables, the mean is the subtraction of the means, while the standard deviation is the square root of the sum of the variances.
The mean and standard deviation for the before treatment were 168.6 and 9.3, respectively. The mean and standard deviation for the after treatment were 137.2 and 7.4.
This means that
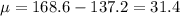
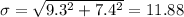
90% confidence interval:
We have that to find our
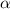 level, that is the subtraction of 1 by the confidence interval divided by 2. So:
level, that is the subtraction of 1 by the confidence interval divided by 2. So:
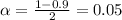
Now, we have to find z in the Ztable as such z has a pvalue of
 .
.
That is z with a pvalue of
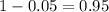 , so Z = 1.645.
, so Z = 1.645.
Now, find the margin of error M as such
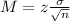
In which
 is the standard deviation of the population and n is the size of the sample.
is the standard deviation of the population and n is the size of the sample.
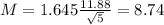
The lower end of the interval is the sample mean subtracted by M. So it is 31.4 - 8.74 = 22.66
The upper end of the interval is the sample mean added to M. So it is 31.4 + 8.74 = 40.14
The 90% confidence interval for the mean reduction in systolic blood pressure is between 22.66 and 40.14.