Solution :
Alternative A Alternative B Alternative C
Annual fixed cost 105000 126000 82000
Variable fixed cost 24 25 37
a). We have to find out the Break even quantity :
Break Even quantity for A

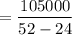
= 3750 units
Break Even quantity for B

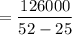
= 4666 units
Break Even quantity for C

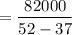
= 5466 units
Therefore, Alternate A has the lowest Break Even quantity.
b). Now,
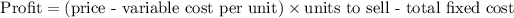
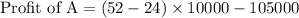
= 280,000 - 105,000
= 175,000
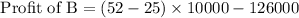
= 270,000 - 126,000
= 144,000

= 150,000 - 105,000
= 45,000
Thus, alternate A has the highest amount of profit.
c).
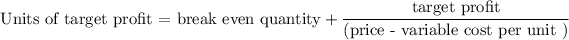
Units of the target profit for A
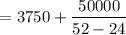
= 5535 units
Units of the target profit for B
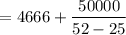
= 6517 units
Units of the target profit for C
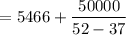
= 8799 units
Thus Alternative A will require the lowest volume of the output.