Answer:
a) The y-component of velocity just before the ball hits the ground is -14.860 meters per second.
b) The ball is in the air during approximately 2.890 seconds.
c) The horizontal distance covered by the ball is 32.695 meters.
d) The magnitude of the velocity of the ball just before it hits the ground is approximately 18.676 meters per second.
e) The angle of the total velocity of the ball just before it hits the ground is approximately 52.717º below the horizontal.
Step-by-step explanation:
a) The ball experiments a parabolic motion, which is a combination of horizontal motion at constant velocity and vertical motion at constant acceleration. First, we calculate the time taken by the ball to hit the ground:
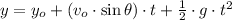 (1)
(1)
Where:
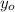 ,
,
 - Initial and final vertical position, measured in meters.
- Initial and final vertical position, measured in meters.
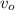 - Initial speed, measured in meters per second.
- Initial speed, measured in meters per second.
 - Launch angle, measured in sexagesimal degrees.
- Launch angle, measured in sexagesimal degrees.
 - Gravitational acceleration, measured in meters per square second.
- Gravitational acceleration, measured in meters per square second.
 - Time, measured in seconds.
- Time, measured in seconds.
If we know that
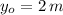 ,
,
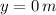 ,
,
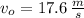 ,
,
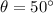 and
and
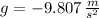 , then the time taken by the ball is:
, then the time taken by the ball is:
 (2)
(2)
This second order polynomial can be solved by Quadratic Formula:
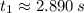 and
and
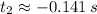
Only the first root offers a solution that is physically reasonable. That is,
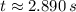 .
.
The vertical velocity of the ball is calculated by this expression:
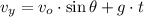 (3)
(3)
Where:
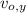 ,
,
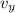 - Initial and final vertical velocity, measured in meters per second.
- Initial and final vertical velocity, measured in meters per second.
If we know that
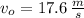 ,
,
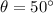 ,
,
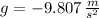 and
and
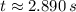 , then the final vertical velocity is:
, then the final vertical velocity is:
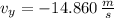
The y-component of velocity just before the ball hits the ground is -14.860 meters per second.
b) From a) we understand that ball is in the air during approximately 2.890 seconds.
c) The horizontal distance covered by the ball (
 ) is determined by the following expression:
) is determined by the following expression:
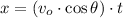 (4)
(4)
If we know that
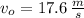 ,
,
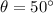 and
and
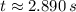 , then the distance covered by the ball is:
, then the distance covered by the ball is:
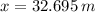
The horizontal distance covered by the ball is 32.695 meters.
d) The magnitude of the velocity of the ball just before hitting the ground (
 ), measured in meters per second, is determined by the following Pythagorean identity:
), measured in meters per second, is determined by the following Pythagorean identity:
 (5)
(5)
If we know that
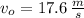 ,
,
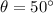 and
and
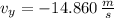 , then the magnitude of the velocity of the ball is:
, then the magnitude of the velocity of the ball is:
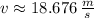 .
.
The magnitude of the velocity of the ball just before it hits the ground is approximately 18.676 meters per second.
e) The angle of the total velocity of the ball just before it hits the ground is defined by the following trigonometric relationship:
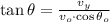
If we know that
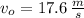 ,
,
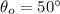 and
and
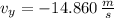 , the angle of the total velocity of the ball just before hitting the ground is:
, the angle of the total velocity of the ball just before hitting the ground is:
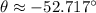
The angle of the total velocity of the ball just before it hits the ground is approximately 52.717º below the horizontal.