Question

What is the ratio in which the point P(3/4,5/12) decides the line segment joining points A(1/2,3/2) and B(2,-5)

​

Answer 1

Given:

The point
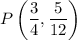`P\left((3)/(4),(5)/(12)\right)` divides the line segment joining points
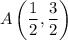`A\left((1)/(2),(3)/(2)\right)` and
`B(2,-5)`.

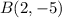To find:

The ratio in which he point P divides the segment AB.

Solution:

Section formula: If a point divides a segment in m:n, then the coordinates of that point are,

`Point=\left((mx_2+nx_1)/(m+n),(my_2+ny_1)/(m+n)\right)`

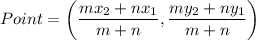
Let point P divides the segment AB in m:n. Then by using the section formula, we get

`\left((3)/(4),(5)/(12)\right)=\left((m(2)+n((1)/(2)))/(m+n),(m(-5)+n((3)/(2)))/(m+n)\right)`

`\left((3)/(4),(5)/(12)\right)=\left((2m+(n)/(2))/(m+n),(-5m+(3n)/(2))/(m+n)\right)`

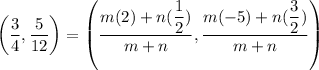
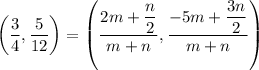
On comparing both sides, we get

`(3)/(4)=(2m+(n)/(2))/(m+n)`

`(3)/(4)(m+n)=(4m+n)/(2)`

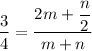
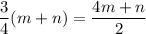
Multiply both sides by 4.

`3(m+n)=2(4m+n)`

`3m+3n=8m+2n`

`3n-2n=8m-3m`

`n=5m`

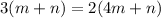
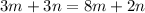
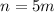
It can be written as

`(1)/(5)=(m)/(n)`

`1:5=m:n`

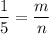
Therefore, the point P divides the line segment AB in 1:5.