Answer:
The error is;
B. Kimberly did not find the inverse sine of the value she calculated
Explanation:
The given parameters of the triangle ΔLMN are;
 = 16
= 16
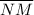 = 10
= 10
∠L = 33°
By sine rule, we have;

Given that ∠L = 33°, we have;

Therefore, we have;
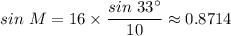
sin M ≈ 0.8714
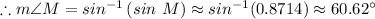
Therefore, m∠M ≈ 60.62°
m∠M ≠ sin M ≈ 0.8714
Therefore;
Kimberly did not find the inverse sine (sin⁻¹) of the value she calculated