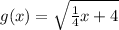Question

Look at the picture for the question.

Answer 1

`g(x) = \sqrt{(1)/(4)x +4}`

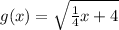
Explanation:

Given

`f(x) = \sqrt{x + 2`

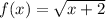
Transformations:

1. Horizontal shrink by 1/4

2. Translation 2 units right

Required

Determine the new function

1. Horizontal shrink by 1/4

This implies that:

For:

`f(x) = \sqrt{x + 2`

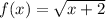
After shrinking, the function is:

`f'((1)/(4)x) = \sqrt{(1)/(4)x + 2}`

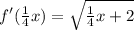
2. Translation 2 units right

For:

`f'((1)/(4)x) = \sqrt{(1)/(4)x + 2}`

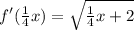
The right translation is given by:

`g(x) = f(x + b)`

Where b is the number of units translated.

So:

`g(x) = f`

`g(x) = f`

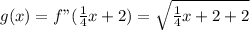
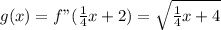
Hence:

`g(x) = \sqrt{(1)/(4)x +4}`