Question

[repost with picture] question #4, show steps please

Answer choices:
A) 2 only
B) 4 only
C) 2 and 5 only
D) 2, 4, and 5
E) 0, 4, and 6

Answer 1

C

Explanation:

We are given the graph of f and that:

`\displaystyle g(x)=\int_0^xf(t)\, dt`

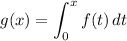
And we want to determine the values of x for which g has a point of inflection.

By the Fundamental Theorem of Calculus:

`g'(x)=f(x)`

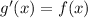
Thus:

`g''(x)=f'(x)`

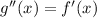
g(x) has a point of inflection if and only if g''(x) = 0 and g''(x) changes signs around the point.

Since g''(x) = f'(x), g''(x) = 0 when f'(x) is 0. This happens at x = 2 and x = 5.

And at both x = 2 and x = 5, f'(x) changes signs before and after. Thus, g''(x) has inflection points at both x = 2 and x = 5.

The correct answer is C.