Question

Math question #1 please show steps

Answer 1

C

Explanation:

An approximation of an integral is given by:

`\displaystyle \int_a^bf(x)\, dx\approx \sum_(k=1)^nf(x_k)\Delta x\text{ where } \Delta x=(b-a)/(n)`

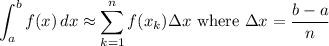
First, find Δx. Our a = 2 and b = 8:

`\displaystyle \Delta x=(8-2)/(n)=(6)/(n)`

The left endpoint is modeled with:

`x_k=a+\Delta x(k-1)`

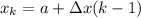
And the right endpoint is modeled with:

`x_k=a+\Delta xk`

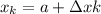
Since we are using a Left Riemann Sum, we will use the first equation.

Our function is:

`f(x)=\cos(x^2)`

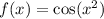
Therefore:

`f(x_k)=\cos((a+\Delta x(k-1))^2)`

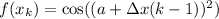
By substitution:

`\displaystyle f(x_k)=\cos((2+(6)/(n)(k-1))^2)`

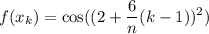
Putting it all together:

`\displaystyle \int_2^8\cos(x^2)\, dx\approx \sum_(k=1)^(n)\Big(\cos((2+(6)/(n)(k-1))^2)\Big)(6)/(n)`

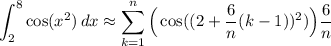
Thus, our answer is C.

*Note: Not sure why they placed the exponent outside the cosine. Perhaps it was a typo. But C will most likely be the correct answer regardless.