Question

What is the asymptote for the function?
I tried to do it but I can’t

Answer 1

Horizontal Asymptote → y = 17

Explanation:

Given function is f(x) =
`(2)/(5)(16)^(x+13)+17`

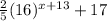
Here, the parent function is g(x) =
`(2)/(5)(16)^x`

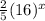
Parent function has a horizontal asymptote as y = 0

If the function g(x) is shifted 13 units left and 17 units up, new function will be f(x) =
`(2)/(5)(16)^(x+13)+17`

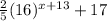
When the parent function is shifted 17 units up, horizontal asymptote shifts 17 units upwards.

Therefore, horizontal asymptote of the image function becomes y = 17.