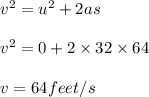Answer:
(a) v = 32 t
h = 16 t^2
g = 32 ft/s^2
(b) 64 ft/s
Step-by-step explanation:
height, h = 64 feet
g = - 32 ft/s^2
(a) Let the time is t .
Let the velocity after time t is v.
Use first equation of motion
v = u + at
- v = 0 - 32 t
v = 32 t
Let the distance is h from the top.
Use second equation of motion
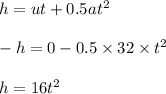
The acceleration is constant for entire motion.
(b) Let the velocity is v as it hits the ground. Use third equation of motion