Question

Car B is traveling a distance dd ahead of car A. Both cars are traveling at 60 ft/s when the driver of B suddenly applies the brakes, causing his car to decelerate at ft/s^2. It takes the driver of car A 0.75 s to react (this is the normal reaction time for drivers). When he applies his brakes, he decelerates at 18 ft/s^2.

Required:
Determine the minimum distance d between the cars so as to avoid a collision.

Answer 1

Step-by-step explanation:

Using the kinematics equation
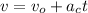`v = v_o + a_ct` to determine the velocity of car B.

where;

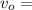`v_o =` initial velocity

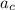`a_c` = constant deceleration

Assuming the constant deceleration is = -12 ft/s^2

Also, the kinematic equation that relates to the distance with the time is:

`S = d + v_ot + (1)/(2)at^2`

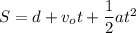
Then:

`v_B = 60-12t`

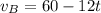
The distance traveled by car B in the given time (t) is expressed as:

`S_B = d + 60 t - (1)/(2)(12t^2)`

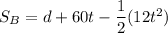
For car A, the needed time (t) to come to rest is:

`v_A = 60 - 18(t-0.75)`

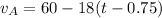
Also, the distance traveled by car A in the given time (t) is expressed as:

`S_A = 60 * 0.75 +60(t-0.75) -(1)/(2)*18*(t-0.750)^2`

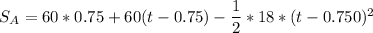
Relating both velocities:

`v_B = v_A`

`60-12t = 60 - 18(t-0.75)`

`60-12t =73.5 - 18t`

`60- 73.5 = - 18t+ 12t`

`-13.5 =-6t`

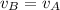
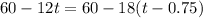
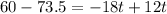
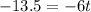
t = 2.25 s

At t = 2.25s, the required minimum distance can be estimated by equating both distances traveled by both cars

i.e.

`S_B = S_A`

`d + 60 t - (1)/(2)(12t^2) = 60 * 0.75 +60(t-0.75) -(1)/(2)*18*(t-0.750)^2`

`d + 60 (2.25) - (1)/(2)(12*(2.25)^2) = 60 * 0.75 +60((2.25)-0.75) -(1)/(2)*18*((2.25)-0.750)^2`

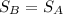
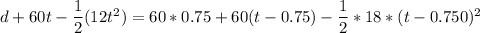
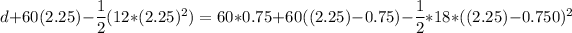
d + 104.625 = 114.75

d = 114.75 - 104.625

d = 10.125 ft