Question

What are the ordered pairs of the

solutions for this system of equations?
f(x) = x2 – 5x + 3; f(x) = -3

Answer 1

Start by writing the system down, I will use
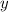`y` to represent
`f(x)`

`y=x^2-5x+3\wedge y=-3`

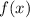
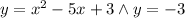
Substitute the fact that
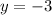`y=-3` into the first equation to get,

`-3=x^2-5x+3`

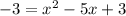
Simplify into a quadratic form (
`ax^2+bx+c=0`),

`x^2-5x+6=0`

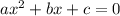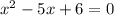
Now you can use Vieta's rule which states that any quadratic equation can be written in the following form,

`x^2+x(m+n)+mn=0`

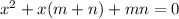
which then must factor into

`(x+m)(x+n)=0`

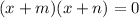
And the solutions will be
`m,n`.

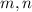Clearly for small coefficients like ours
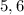`5,6`, this is very easy to figure out. To get 5 and 6 we simply say that
`m=3, n=2`.

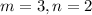This fits the definition as
`5=3+2` and
`6=2\cdot3`.

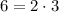So as mentioned, solutions will equal to
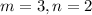`m=3, n=2` but these are just x-values in the solution pairs of a form
`(x,y)`.

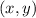To get y-values we must substitute 3 for x in the original equation and then also 2 for x in the original equation. Luckily we already know that substituting either of the two numbers yields a zero.

So the solution pairs are
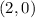`(2,0)` and
`(3,0)`.

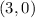Hope this helps :)