The angle the Leaning Tower of Pisa makes with the ground is approximately
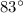 when rounded to the nearest whole degree.
when rounded to the nearest whole degree.
How did we get the value?
To find the angle that the Leaning Tower of Pisa makes with the ground, you can use trigonometry. The tangent of an angle in a right triangle is defined as the ratio of the length of the opposite side to the length of the adjacent side.
Let
 be the height the tower makes with the ground, and
be the height the tower makes with the ground, and
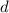 be the horizontal distance from the base of the tower to the point where the rock lands.
be the horizontal distance from the base of the tower to the point where the rock lands.
The tangent of the angle
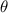 is given by:
is given by:
![\[ \tan(\theta) = (h)/(d) \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/y3a4c5xhk3tf45771b6m1oztm0ijuuscuc.png)
Given that the rock falls 182 feet and lands 22 feet from the base, we have
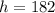 and
and
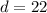 . Plug these values into the formula:
. Plug these values into the formula:
![\[ \tan(\theta) = (182)/(22) \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/mkzny4j2fc35eyquudlfqmhy3w0ts06u49.png)
Now, calculate the arctangent (inverse tangent) of this value to find the angle
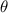 :
:
![\[ \theta = \arctan\left((182)/(22)\right) \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/2jmkkj2g37by42f5q3dkia2cuktdpl5hwo.png)
![\[ \theta = \arctan\left(8.2727}\right) \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/mkypcsz8zmsuqzj5s5xs8onvn7w4f6huw7.png)
Therefore, the angle the Leaning Tower of Pisa makes with the ground is approximately
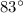 when rounded to the nearest whole degree.
when rounded to the nearest whole degree.