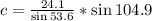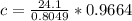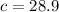Question

Solve the triangle. Round to the nearest tenth when necessary or to the nearest minute as appropriate. B = 53.6° C = 104.9° b = 24.1 A = 21.5°, a = 11, c = 28.9 A = 21.5°, a = 13, c = 30.9 A = 19.5°, a = 28.9, c = 11 A = 19.5°, a = 30.9, c = 13

Answer 1

`a =11.0`

`\angle A =21.5^o`

`c = 28.9`

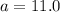
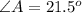
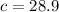
Explanation:

Given

`\angle B = 53.6^o`

`\angle C = 104.9^o`

`b=24.1`

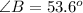
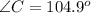
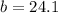
Required

Solve the triangle

We have:

`\angle A + \angle B + \angle C =180^o` --- angles in a triangle

Substitute known values

`\angle A + 53.6^o + 104.9^o =180^o`

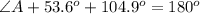
So, we have:

`\angle A =180^o-53.6^o - 104.9^o`

`\angle A =21.5^o`

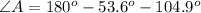
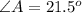
To solve for the sides, we make use of sine rule:

`(a)/(\sin A) =(b)/(\sin B) = (c)/(\sin C)`

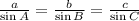
So, we have:

`(a)/(\sin (21.5)) =(24.1)/(\sin 53.6) = (c)/(\sin 104.9)`

Solving for (a), we have:

`(a)/(\sin (21.5)) =(24.1)/(\sin 53.6)`

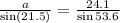
Make (a) the subject

`a =(24.1)/(\sin 53.6) * \sin (21.5)`

`a =(24.1)/(0.8049) * 0.3665`

`a =11.0`

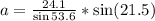
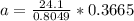
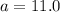
To solve for (c), we have:

`(24.1)/(\sin 53.6) = (c)/(\sin 104.9)`

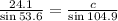
Make (c) the subject

`c = (24.1)/(\sin 53.6) * \sin 104.9`

`c = (24.1)/(0.8049) * 0.9664`

`c = 28.9`