Answer:
HT = 17 cm
<T = 58°
<H = 32°
Explanation:
✔️Find HT:
Since it's a right triangle, we would apply the Pythagorean Theorem given as c² = a² + b²
Where,
a = HW = 15 cm
b = WT = 8 cm
c = HT
Plug in the values:
HT² = 15² + 8²
HT² = 289
HT = √289
HT = 17 cm
✔️Find <T by applying trigonometric ratio formula:
Recall: SOH CAH TOA
Reference angle (θ) = <T
HW = 15 cm = Opposite side length
WT = 8 cm = Adjacent side length
Apply CAH:
Cos θ = Adj/Hyp
Substitute
Cos T = 8/15
T =
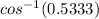
T ≈ 58°
✔️Find <H:
Sun of interior angles of a triangle = 180°
Therefore,
m<H + m<T + m<W = 180°
Substitute
m<H + 58° + 90° = 180°
m<H + 148° = 180°
m<H = 180° - 148°
m<H = 32°