Question

An area of a rectangle is x^2-10x+21, determine the dimensions (length and width) of the rectangle , if x=8cm

Answer 1

In order to determine the dimensions (length and width) of the rectangle, we first have to resolve the area; x²-10x+21, which is a quadratic equation. And by doing so, we'll have:

x² - 10x + 21 = (x - 7)(x - 3)

Given that x = 8cm, the length, l = {8 - 7} = 1cm

and the width, w = {8 - 3} = 5cm

Explanation:

To resolve the area: x² - 10x + 21, we have that:

`{x}^(2) - 10x + 21 \\ = {x}^(2) - 7x - 3x + 21 \\ = x(x - 7) - 3(x \: - 7) \\ = (x - 7)(x - 3).`

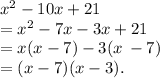
From the above solution, to find the dimensions of the rectangle, we will substitute the given value of x (x = 8) into the solution set (x - 7)(x - 3).

`length = (x - 7) \\ = 8 - 7 \\ = 1cm.`

Also, to find the width, we have:

`width = (x - 3) \\ = 8 - 3 \\ = 5cm.`

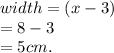
Therefore, the dimensions of the rectangle are length = 1cm and width = 5cm.