Question

Aaron owns a rare baseball card. He bought the card for $7.50 in 1987 and it's value increases by 6% each year. Write and use an exponential growth function to find the baseball cards value in 2015

Answer 1

1) The expression growth function is f(x) = a·(1 + r)ˣ

2) The baseball card's value in 2015 is approximately $38.337650

Explanation:

1) An exponential growth function, 'f(x)', has the following general form;

f(x) = a·(1 + r)ˣ

Where;

a = The initial amount

r = The growth rate

x = The count of time periods

The given parameters are;

The initial amount Aaron bought the rare baseball card, a = $7.50

The percentage by which the value increase each year, r = 6% each year

The number of years the baseball card increases in value, x = 2015 - 1987 = 28 years

2) Plugging in the values in the function for exponential growth gives;

f(x) = a·(1 + r)ˣ

∴ f(28) = 7.50 × (1 + 6/100)²⁸ =
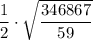`(1)/(2) \cdot \sqrt{(346867)/(59) }`≈ 38.337650

The baseball card's value in 2015 ≈ $38.337650