Question

In ΔABC, m < B = 22°, m < C = 52° and a = 30. Find the length of b to the nearest tenth.

Answer 1

The length of
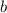`b` is approximately 11.7.

Explanation:

The sum of internal angles in triangles equals 180°, as we know the measures of angles B and C, we determine the measure of angle A by algebraic means:

`A = 180^(\circ)-B-C` (1)

(
`B = 22^(\circ)`,
`C = 52^(\circ)`)

`A = 180^(\circ)-22^(\circ)-52^(\circ)`

`A = 106^(\circ)`

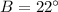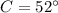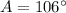
The length of
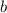`b` is found by the Law of Sine:

`(b)/(\sin B) = (a)/(\sin A)`

`b = a\cdot \left((\sin B)/(\sin A) \right)`

(
`a = 30`,
`A = 106^(\circ)`,
`B = 22^(\circ)`)

`b = 30\cdot \left((\sin 22^(\circ))/(\sin 106^(\circ)) \right)`

`b \approx 11.7`

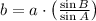
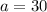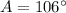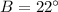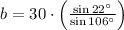
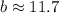
The length of
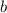`b` is approximately 11.7.