Answer:
(a) -12
General Formulas and Concepts:
Pre-Algebra
Order of Operations: BPEMDAS
- Brackets
- Parenthesis
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
Equality Properties
- Multiplication Property of Equality
- Division Property of Equality
- Addition Property of Equality
- Subtraction Property of Equality
Calculus
Integrals
Integration Rule [Reverse Power Rule]:
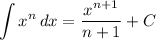
Integration Property [Swapping Limits]:
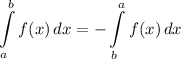
Integration Property [Multiplied Constant]:
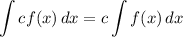
Integration Property [Addition/Subtraction]:
![\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx](https://img.qammunity.org/2022/formulas/mathematics/high-school/r5yh324r81plt97j3zrr5qi2xxczxlqi34.png)
Integration Property [Splitting Integral]:
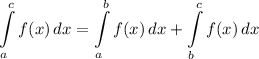
Integration Rule [Fundamental Theorem of Calculus 1]:
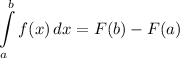
Explanation:
Step 1: Define
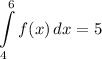
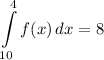
![\displaystyle \int\limits^(10)_6 {[4f(x) + 10]} \, dx](https://img.qammunity.org/2022/formulas/mathematics/high-school/qe523jcl0ekb735eslr2urn9wkcst91eht.png)
Step 2: Solve Pt. 1
- [Integral] Rewrite [Integration Property - Addition]:
![\displaystyle \int\limits^(10)_6 {[4f(x) + 10]} \, dx = \int\limits^(10)_6 {4f(x)} \, dx + \int\limits^(10)_6 {10} \, dx](https://img.qammunity.org/2022/formulas/mathematics/high-school/765rdcaekfkbfzny5n2mw2ugi2ceig780c.png)
- [Integral] Rewrite [Integration Property - Multiplied Constant]:
![\displaystyle \int\limits^(10)_6 {[4f(x) + 10]} \, dx = 4\int\limits^(10)_6 {f(x)} \, dx + 10\int\limits^(10)_6 {} \, dx](https://img.qammunity.org/2022/formulas/mathematics/high-school/an9o7yvj5vvi7v917hsa8shk4bau7c1rwz.png)
Step 3: Redefine
Manipulate the given integral values.
- [Integrals] Combine [Integration Property - Splitting Integral]:
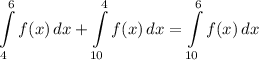
- [Integral] Rewrite:
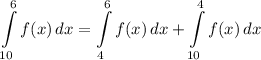
- [Integral] Substitute in integrals:
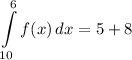
- [Integral] Add:
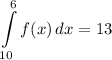
- [Integral] Rewrite [Integration Property - Swapping Limits]:
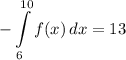
- [Integral] [Division Property of Equality] Isolate integral:
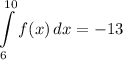
Step 4: Solve Pt. 2
- [Integral] Substitute in integral:
![\displaystyle \int\limits^(10)_6 {[4f(x) + 10]} \, dx = 4(-13) + 10\int\limits^(10)_6 {} \, dx](https://img.qammunity.org/2022/formulas/mathematics/high-school/ke5p1cz9kmrjlzuomznzzj3ytg4z4qzzex.png)
- [Integral] Integrate [Integration Rule - Reverse Power Rule]:
![\displaystyle \int\limits^(10)_6 {[4f(x) + 10]} \, dx = 4(-13) + 10(x) \bigg| \limits^(10)_6](https://img.qammunity.org/2022/formulas/mathematics/high-school/pdacp4g4m9e2gj2shg9y1ln4hagilvtt2y.png)
- [Integral] Evaluate [Integration Rule - FTC 1]:
![\displaystyle \int\limits^(10)_6 {[4f(x) + 10]} \, dx = 4(-13) + 10(10 - 6)](https://img.qammunity.org/2022/formulas/mathematics/high-school/n8uv8mcctihcvmqqyuwuzpsm0kbbtddkg3.png)
- [Integral] (Parenthesis) Subtract:
![\displaystyle \int\limits^(10)_6 {[4f(x) + 10]} \, dx = 4(-13) + 10(4)](https://img.qammunity.org/2022/formulas/mathematics/high-school/zsvwc0hwazlg0aew708gpftp3ayqjkepy4.png)
- [Integral] Multiply:
![\displaystyle \int\limits^(10)_6 {[4f(x) + 10]} \, dx = -52 + 40](https://img.qammunity.org/2022/formulas/mathematics/high-school/m1x3vstwc7aw8ihbqvqz9vg8e2rkgko3oh.png)
- [Integral] Add:
![\displaystyle \int\limits^(10)_6 {[4f(x) + 10]} \, dx = -12](https://img.qammunity.org/2022/formulas/mathematics/high-school/gn81t4rjkj0nlj2wfag5u2t8sgyodzc65o.png)
Topic: AP Calculus AB/BC
Unit: Integration
Book: College Calculus 10e