Question

You work with the office of city planning which is currently evaluating a new contract for a major highway. The chosen contractor claims that the roads they build usually have a single (1) defect per 50 miles of road, assume this follows a Poisson distribution. The portion of highway that your city is building is 30 miles long.

What is the probability that there are no (0) defects in the completed highway?

Answer 1

0.5488 = 54.88% probability that there are no defects in the completed highway.

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given interval.

The portion of highway that your city is building is 30 miles long.

The mean is one defect per 50 miles. Since the highway is 30 miles, we have that:

`\mu = (30)/(50) = 0.6`

What is the probability that there are no (0) defects in the completed highway?

This is P(X = 0). So

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 0) = (e^(-0.6)*0.6^(0))/((0)!) = 0.5488`

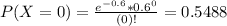
0.5488 = 54.88% probability that there are no defects in the completed highway.