Question

A curve is represented by the parametric equations x=t , y=3t^2 find the area under the curve from t=1 to t=2

Answer 1

`\displaystyle A = 7`

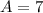
General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Pre-Calculus

• Parametric to Rectangular Form Conversion

Calculus

Integrals - Area under the curve

Area of a Curve Formula:
`\displaystyle A = \int\limits^b_a {f(x)} \, dx`

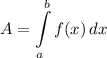
Integration Rule [Reverse Power Rule]:
`\displaystyle \int {x^n} \, dx = (x^(n + 1))/(n + 1) + C`

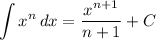
Integration Property [Multiplied Constant]:
`\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx`

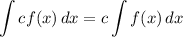
Integration Rule [Fundamental Theorem of Calculus 1]:
`\displaystyle \int\limits^b_a {f(x)} \, dx = F(b) - F(a)`

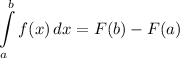
Explanation:

*Note:

The area under the curve is essentially the definition of an integral.

Step 1: Define

Parametric

x = t

y = 3t²

1 ≤ t ≤ 2

Step 2: Rewrite

Rewrite parametric to rectangular form and change bounds of integration.

1. [Parametric] Substitute in t: y = 3x²
2. [Parametric] Plug in values of t [Bounds]: 1 ≤ x ≤ 2

Step 3: Find Area

Integration.

1. Substitute in variables/function [Area]:
   `\displaystyle A = \int\limits^2_1 {3x^2} \, dx`
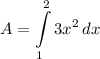
2. [Area] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle A = 3\int\limits^2_1 {x^2} \, dx`
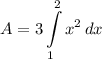
3. [Area] Integrate [Integration Rule - Reverse Power Rule]:
   `\displaystyle A = 3((x^3)/(3)) \bigg| \limit^2_1`
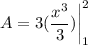
4. [Area] Evaluate [Integration Rule - Fundamental Theory of Calculus 1]:
   `\displaystyle A = 3((2^3)/(3) - (1^3)/(3))`
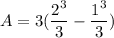
5. [Area] (Parenthesis) [Fraction] Evaluate exponents:
   `\displaystyle A = 3((8)/(3) - (1)/(3))`
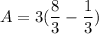
6. [Area] (Parenthesis) Subtract:
   `\displaystyle A = 3((7)/(3))`
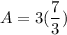
7. [Area] Multiply:
   `\displaystyle A = 7`

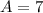
Topic: AP Calculus AB/BC

Unit: Area under the curve

Book: College Calculus 10e