Question

Help please!!

Calculate a student's weight (70 kg) on Earth using the Universal Gravitational Law



Calculate a student's weight (70 kg) on Mercury using the Universal Gravitational Law



Calculate a student's weight (70 kg) on the Sun using the Universal Gravitational Law

Answer 1

1) The student's weight on Earth is approximately 687.398 N

2) The student's weight on Mercury is approximately 257.85 N

3) The student's weight on the Sun is approximately 19,164.428 N

Step-by-step explanation:

The mass of the student, m = 70 kg

1) The mass of the Earth, M = 5.972 × 10²⁴ kg

The radius of the Earth, R = 6,371 km = 6.371 × 10⁶ m

The universal gravitational constant, G = 6.67430 × 10⁻¹¹ N·m²/kg²

Mathematically, the universal gravitational law is given as follows;

`F_g =G * (M \cdot m)/(R^(2))`

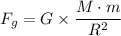
Therefore, we have;

`F_g=6.67430 * 10^(-11) * (5.972 * 10^(24) \cdot 70)/((6.371 * 10^6)^(2)) \approx 687.398`

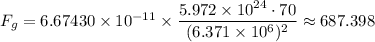
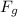`F_g` = W ≈ 687.398 N

The student's weight on Earth, W ≈ 687.398 N

2) On Mercury, we have;

The mass of Mercury, M₂ = 3.285 × 10²³ kg

The radius of Mercury, R₂ = 2,439.7 km = 2.4397 × 10⁶ m

The universal gravitational constant, G = 6.67430 × 10⁻¹¹ N·m²/kg²

The universal gravitational law is
`F_g =G * (M_2 \cdot m)/(R_2^(2))`

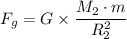
Therefore, we have;

`F_g=6.67430 * 10^(-11) * (3.285 * 10^(23) \cdot 70)/((2.4397 * 10^6)^(2)) \approx 257.85`

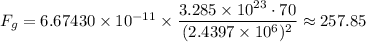
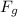`F_g` = W₂ ≈ 257.85 N

The student's weight on Mercury, W₂ ≈ 257.85 N

3) On the Sun, we have;

The mass of the Sun, M₃ ≈ 1.989 × 10³⁰ kg

The radius of the Sun, R₃ ≈ 696,340 km = 6.9634 × 10⁸ m

The universal gravitational constant, G = 6.67430 × 10⁻¹¹ N·m²/kg²

The universal gravitational law is
`F_g =G * (M_3 \cdot m)/(R_3^(2))`

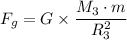
Therefore, we have;

`F_g=6.67430 * 10^(-11) * (1.989 * 10^(30) \cdot 70)/((6.9634 * 10^8)^(2)) \approx 19,164.428`

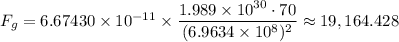
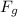`F_g` = W₃ ≈ 19,164.428 N

The student's weight on the Sun, W₃ ≈ 19,164.428 N