Question

PLEASE HELP!!!!!!!!!!!! VOLUME OF A CONE!!!!!!

Answer 1

Hi! Your answer is 125/3 π

Please see an explanation for a clear understanding to the problem.

Any questions about the answer/explanation can be asked through comments! :)

Explanation:

For this problem, I'll be demonstrating two methods to solve your problem which are Integration method and Formula method. Let's start with Formula method first!

Formula Method

Volume of Cone Formula

`V=\huge{(1)/(3)\pi r^2h}`

r is a radius. Therefore, r² is a diameter.

h is height of cone.

Our r is 5. Therefore, 5² = 25.

Our h is 5.

Substitute these values in the equation.

`V=\huge{(1)/(3)\pi (5)^2(5)}\\V=\huge{(1)/(3)\pi (25)(5)} \\V=\huge{(1)/(3)\pi (125)}\\V=\huge{(125)/(3)\pi}`

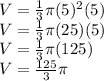
Hence, the volume of a cone is 125/3 pi. If you want in Mixed Number form then It'd be 41 and 2/3 pi [ 41 2/3 pi]

Integration Method - Proof

Let r':r = x:h

Therefore,

`\huge{(r')/(r)=(x)/(h)}\\\huge{r'=(x)/(h)r`

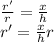
r and h both are same (r is still radius while h is still height)

`\huge{S(x)=\pi(r')^2`

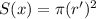
The reason why we add pi because the surface is a circle. If the surface is not a circle, we don't add pi.

`\huge{S(x)=\pi((x)/(h)r)^2}\\\huge{S(x)=\pi((x^2r^2)/(h^2))}\\\huge{S(x)=(\pi r^2)/(h^2)x^2}\\`

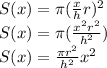
The range starts from 0 ≤ x ≤ h

`\huge{V=\int\limits^h_0 {S(x)} \, dx`

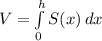
Substitute S(x) in.

`\huge{V=\int\limits^h_0 {(\pi r^2)/(h^2)x^2 } \, dx`

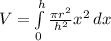
Integrate, separate everything in the integrand out except for x^2

`\huge{V=(\pi r^2)/(h^2) \int\limits^h_0 {x^2} \, dx}\\\huge{V=(\pi r^2)/(h^2)[(1)/(3)x^3]^h__0}}\\\huge{V=(\pi r^2)/(h^2)[(1)/(3)h^3]}\\\huge{V=\pi r^2[(1)/(3)h]}\\\huge{V=(1)/(3)\pi r^2h}`

As you notice, Integration method is pretty useful, but it's mostly for an advanced volume lesson only.

Integration Method - Problem Solving

Let r':r = x:h

r is given as 5

h is given as 5 as well.

Therefore, r':5 = x:5

`\huge{(r')/(5)=(x)/(5)}\\\huge{r'=(x)/(5)(5)}\\r'=x`

`\huge{S(x)=\pi(r')^2}\\\huge{S(x)=\pi(x^2)}\\\huge{S(x)=\pi x^2}`

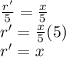
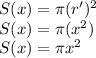
The range of volume starts from surface to height. Therefore the range is 0 ≤ x ≤ 5

`\huge{V=\int\limits^5_0 {S(x)} \, dx }\\\huge{V=\int\limits^5_0 {\pi x^2} \, dx }\\\huge{V=\pi\int\limits^5_0 {x^2} \, dx }\\\huge{V=\pi[(1)/(3)x^3]^5__0}}\\\huge{V=\pi[((1)/(3)(5)^3-(1)/(3)(0)^3]}\\\huge{V=\pi[((1)/(3)(125)-0)]}\\ \huge{V=\pi[((1)/(3)(125)]}\\\huge{V=\pi((125)/(3))}\\\huge{V=(125)/(3)\pi}`

Notice that both methods have same answer. Hence, we can conclude that the volume of a cone is 125/3 pi units²