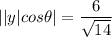Answer:
Explanation:
From the given information:
We can see that:
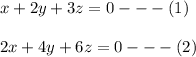
From equation (1), if we multiply it by 2, we will get what we have in equation (2).
It implies that,
x + 2y + 3z = 0 ⇔ 2x + 4y + 6z = 0
And, W satisfies the equation x + 2y + 3z = 0
i.e.
W = {(x,y,z) ∈ R³║x+2y+3z = 0}
Now, to determine the distance through the plane W and point is;
![y = [1 \ 1 \ 1]^T](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/7j0m8zlbs77jaqga9abgmw.png)
Here, the normal vector
![n = [1\ 2\ 3]^T](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/62091dpwhs7ztfrjj1r1vy.png) is related to the plane x + 2y + 3z = 0
is related to the plane x + 2y + 3z = 0
Suppose θ is the angle between the plane W and the point
![y = [1 \ 1 \ 1]^T](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/7j0m8zlbs77jaqga9abgmw.png) , then the distance is can be expressed as:
, then the distance is can be expressed as:

![||y|cos \theta| = ([1 \ 2\ 3 ]^T [1 \ 1 \ 1] ^T)/(√(1^2+2^2+3^2))](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/pwhfcsl0e39g3gsssjrsro.png)
![||y|cos \theta| = ([1+ 2+ 3 ])/(√(1+4+9))](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/l1gw45xkhsxcngt5o2nc23.png)