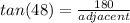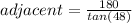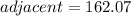Question

Can someone please help

Answer 1

`162.07`

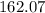
Explanation:

An image that creates represents this situation has been attached to this answer. As one can see, the diagram models the situation, the angle of depression represents the angle between the horizon line and the line of sight. The horizon line and the tower form a right angle (a (90) degree angle). This means that the angle of depression is complementary to the angle of sight. Therefore, one can state the following:

`(angle\ of\ depression) + (angle\ of \ sight)=90`

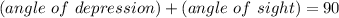
Substitute,

`(angle\ of\ depression) + (angle\ of \ sight)=90`

`(m<ABD)+(m<DBC)=90`

`42+(m<DBC)=90`

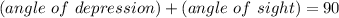
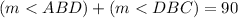
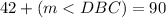
Inverse operations,

`42+(m<DBC)=90`

`m<DBC=48`

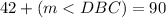
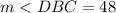
Now one can use the right angle trigonometric ratios to solve this problem. The right angle trigonometric ratios are a series of ratios that describe the relationship between the sides and angles in a right triangle. These ratios are as follows:

`sin(\theta)=(opposite)/(hypotenuse)\\\\cos(\theta)=(adjacent)/(hypotenuse)\\\\tan(\theta)=(opposite)/(adjacent)`

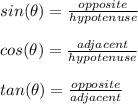
Bear in mind, the terms (opposite) and (adjacent) are subjective, and change depending on the reference angle. However, the term (hypotenuse) refers to the side opposite the right angle and is constant regardless of the reference angle.

In this case, one has found an angle in the triangle, one is given the measure of the side opposite this angle, and one is asked to find the side adjacent to this angle. Therefore, it would make the most sense to use the ratio tangent (tan).

`tan(\theta)=(opposite)/(adjacnet)`

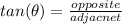
Substitute,

`tan(48)=(180)/(adjacent)`

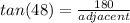
Inverse operations,

`tan(48)=(180)/(adjacent)`

`adjacent=(180)/(tan(48))`

`adjacent=162.07`